Fermat's principle

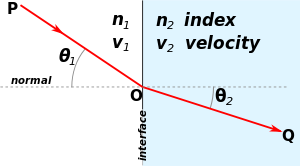
Fermat's principle leads to Snell's law; when the sines of the angles in the different media are in the same proportion as the propagation velocities, the time to get from P to Q is minimized.

In optics, Fermat's principle or the principle of least time is the principle that the path taken between two points by a ray of light is the path that can be traversed in the least time. This principle is sometimes taken as the definition of a ray of light.[1] However, this version of the principle is not general; a more modern statement of the principle is that rays of light traverse the path of stationary, not minimal, time.

Fermat's principle can be used to describe the properties of light rays reflected off mirrors, refracted through different media, or undergoing total internal reflection. It can be deduced from Huygens' principle, and can be used to derive Snell's law of refraction and the law of reflection.

Contents

Modern version

The historical form proposed by French mathematician Pierre de Fermat is incomplete. The modern version of Fermat's principle states that the optical path length must be stationary, which means that it can be either minimal, maximal or a point of inflection (a saddle point). Minima occur when a wave passes from one medium into another (refraction) and in the reflection of light from a planar mirror. Maxima occur in gravitational lensing. A point of inflection describes the path light takes when it is reflected off an elliptical mirrored surface.

History

Hero of Alexandria (Heron) (c. 60) described a principle of reflection, which stated that a ray of light that goes from point A to point B, suffering any number of reflections on flat mirrors, in the same medium, has a smaller path length than any nearby path.[2]

Ibn al-Haytham (Alhacen), in his Book of Optics (1021), expanded the principle to both reflection and refraction, and expressed an early version of the principle of least time. His experiments were based on earlier works on refraction carried out by the Greek scientist Ptolemy[3]

The generalized principle of least time in its modern form was stated by Fermat in a letter dated January 1, 1662, to Cureau de la Chambre[4]. It was met with objections made in May 1662 by Claude Clerselier, an expert in optics and leading spokesman for the Cartesians at that time. Amongst his objections, Clerselier states:

... Fermat's principle can not be the cause, for otherwise we would be attributing knowledge to nature: and here, by nature, we understand only that order and lawfulness in the world, such as it is, which acts without foreknowledge, without choice, but by a necessary determination.

The original French, from Mahoney, is as follows:

Le principe que vous prenez pour fondement de votre démonstration, à savoir que la nature agit toujours par les voies les plus courtes et les plus simples, n’est qu’un principe moral et non point physique, qui n’est point et qui ne peut être la cause d’aucun effet de la nature.

Indeed Fermat's statement does not hold standing alone, as it directly attributes the property of intention and choice to a beam of light. However, Fermat's principle is in fact correct if one considers it to be a result rather than the original cause. On the other hand, considering it a cause makes good sense given what we now know about the modern theory of light (quantum electrodynamics [5]).

Derivation

Classically, Fermat's principle can be considered as a mathematical consequence of Huygens' principle. Indeed, of all secondary waves (along all possible paths) the waves with the extrema (stationary) paths contribute most due to constructive interference. Supposing that light waves propagate from A to B by all possible routes ABj , unrestricted initially by rules of geometrical or physical optics. The various optical paths ABj will vary by amounts greatly in excess of one wavelength, and so the waves arriving at B will have a large range of phases and will tend to interfere destructively. But if there is a shortest route AB0, and the optical path varies smoothly through it, then a considerable number of neighboring routes close to AB0 will have optical paths differing from AB0 by second-order amounts only and will therefore interfere constructively. Waves along and close to this shortest route will thus dominate and AB0 will be the route along which the light is seen to travel.[6]

Fermat's principle can be derived from the main principle of quantum electrodynamics stating that any particle (e.g. a photon or electron) propagates over all possible paths and the interference (sum) of all possible wavefunctions (at the point of observer or detector) gives the correct probability of detection of this particle (at this point). Thus all paths except extremal (shortest, longest or stationary) cancel each other out.

In the classic mechanics of waves, Fermat's principle follows from the extremum principle of mechanics (see variational principle).

See also

Notes

  1. ↑ Arthur Schuster, An Introduction to the Theory of Optics, London: Edward Arnold, 1904 online.
  2. ↑ History of Geometric Optics/Richard Fitzpatrick
  3. ↑ Pavlos Mihas (2005). Use of History in Developing ideas of refraction, lenses and rainbow, Demokritus University, Thrace, Greece.
  4. ↑ Michael Sean Mahoney, The Mathematical Career of Pierre de Fermat, 1601-1665, 2nd edition (Princeton University Press, 1994), p. 401
  5. ↑ Richard Feynman, QED: The strange theory of light and matter, Princeton University Press, 1985.
  6. ↑ Ariel Lipson, Stephen G. Lipson, Henry Lipson, Optical Physics 4th Edition, Cambridge University Press, ISBN 9780521493451.